Score-Debiased Kernel Density Estimation (SD-KDE)

TL;DR

SD-KDE shifts each sample once along an estimated score, then runs standard KDE on the shifted points.
With an exact score, the paper states an improved asymptotic MISE rate compared to classical KDE.
Experiments on 1D and 2D synthetic data (plus an MNIST demo) show improved accuracy over a Silverman-bandwidth baseline.

Problem setting

KDE estimates an unknown density from samples, but performance is sensitive to bandwidth. The paper asks whether score estimates can reduce KDE bias without sacrificing variance too much.

Key idea

Use the score to "undo" part of KDE's smoothing bias:

Shift each sample once in the direction of the estimated score.
Run standard KDE on the shifted samples.

This is the core "shift-then-smooth" idea.

Method (as described)

Inputs:

samples x_1 through x_n
an estimated score function
a kernel and bandwidth

Algorithm:

Shift each point by a small step proportional to h^2 times the score.
Evaluate KDE on the shifted points.

The shift step is:

\tilde{x}_i = x_i + \frac{h^2}{2}\,\hat{s}(x_i)

The paper provides a bias expansion showing that, with an exact score, the leading-order bias term is removed.

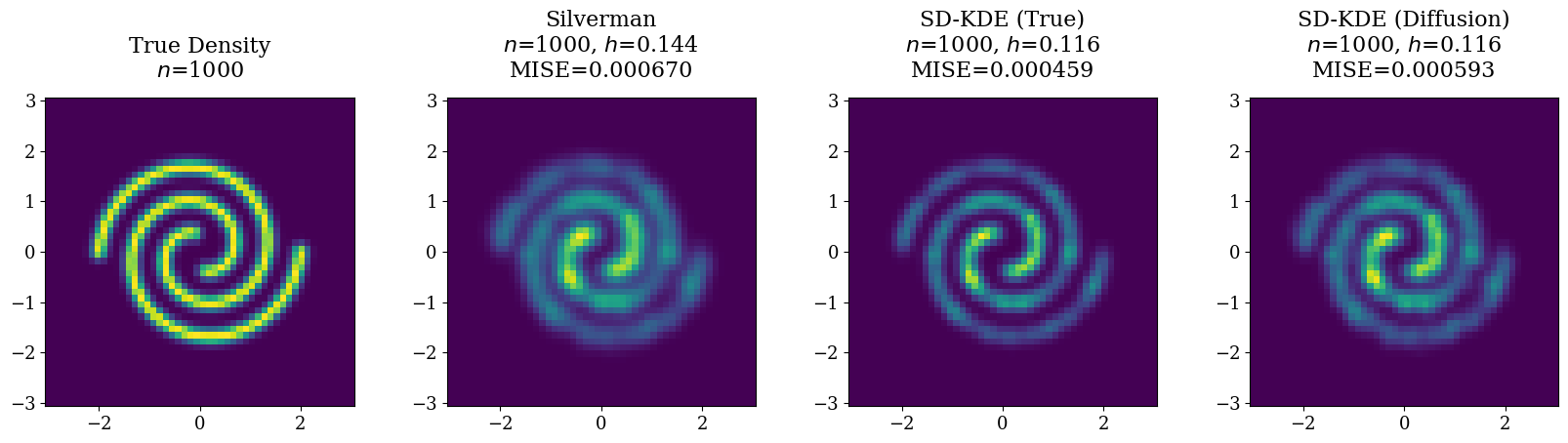
Spiral synthetic example

SD-KDE with oracle score

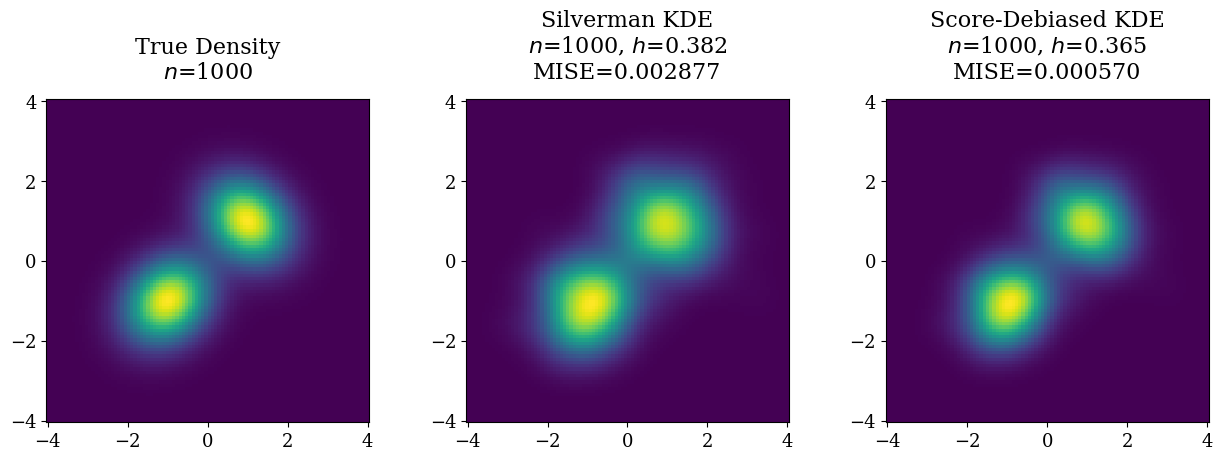
2D mixture of Gaussians (oracle score)

Evidence

The paper reports:

1D Gaussian and Laplace mixture experiments with improved MISE scaling compared to classical KDE.
2D experiments (spiral and Gaussian mixtures) showing gains with an oracle score.
An MNIST demonstration where score estimates come from a DDPM and the resulting density ranking aligns with perceived quality.

With an exact score, the paper states an improved asymptotic rate:

\mathrm{MISE} = \mathcal{O}\left(n^{-8/(d+8)}\right)

Limitations and caveats

The theoretical improvement assumes an exact score, which is rarely available in practice.
When the score is learned, performance depends heavily on the quality of that estimator.
KDE remains sensitive to dimensionality even with bias reduction.

Takeaway

SD-KDE is a clean, theoretically motivated way to reduce KDE bias using score information, with promising synthetic and small-scale empirical evidence.