TL;DR
- SD-KDE improves accuracy but is expensive because of its quadratic score computation.
- Flash-SD-KDE reorganizes the computation to map onto GEMMs, making Tensor Core acceleration possible.
- The paper reports large speedups relative to Torch and scikit-learn baselines on GPU benchmarks.
Problem setting
SD-KDE adds a score-based shift step to KDE, which introduces extra work. The paper's goal is to keep the estimator exact while dramatically reducing runtime on modern GPUs.
Key idea
Rewrite the dominant computations in SD-KDE so they are expressed as matrix multiplications. This makes the work compatible with Tensor Core optimized GEMMs (implemented in Triton).
Method (high level)
- Compute an empirical score for each training point.
- Shift training points using the score.
- Evaluate KDE on the shifted samples.
The Gaussian KDE can be written as:
The key algebraic trick is the dot-product identity:
The implementation avoids storing full pairwise matrices by streaming tiles and accumulating results.
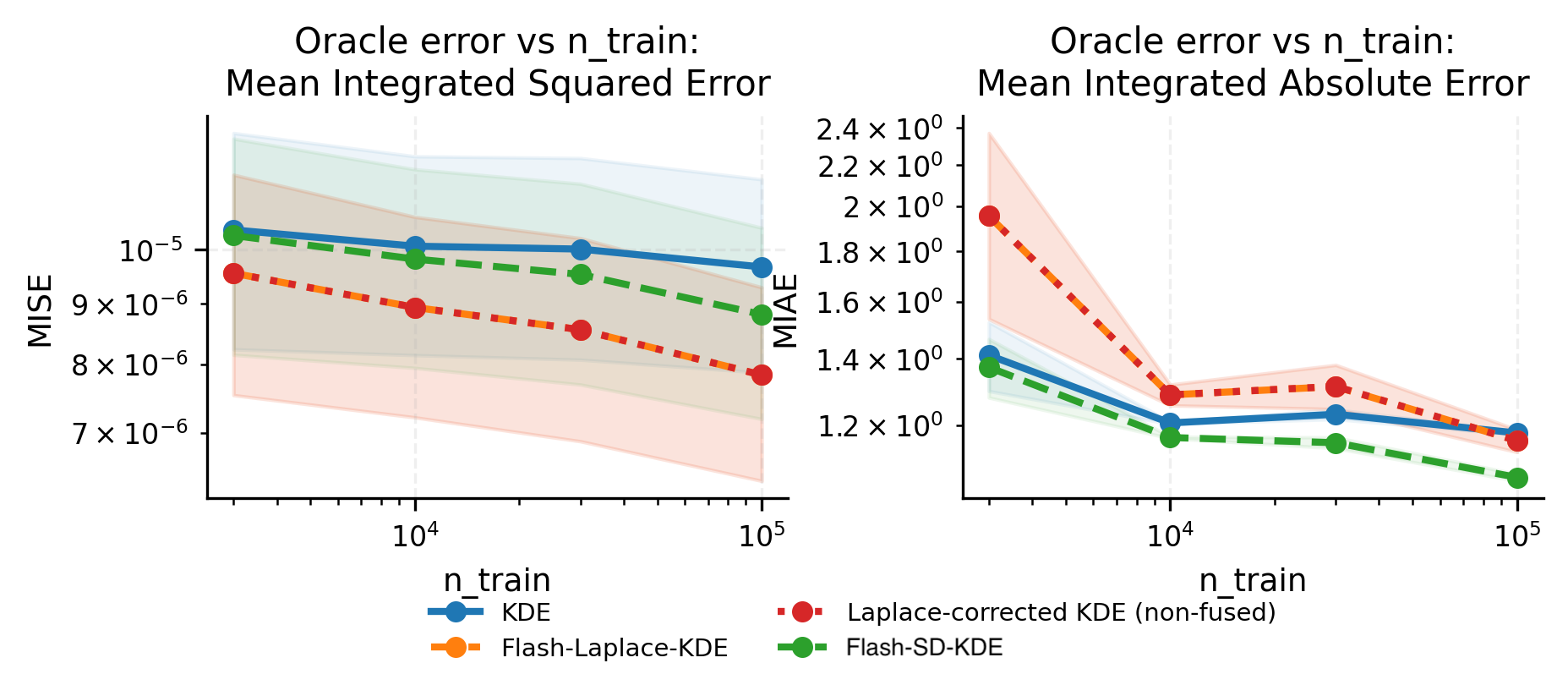
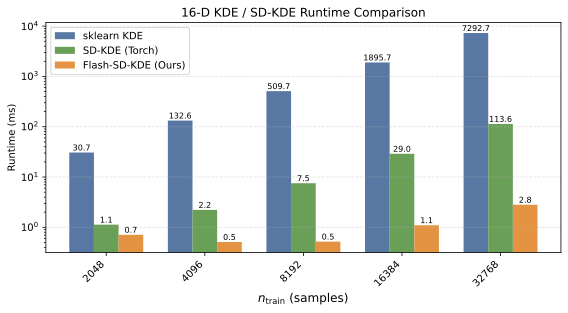
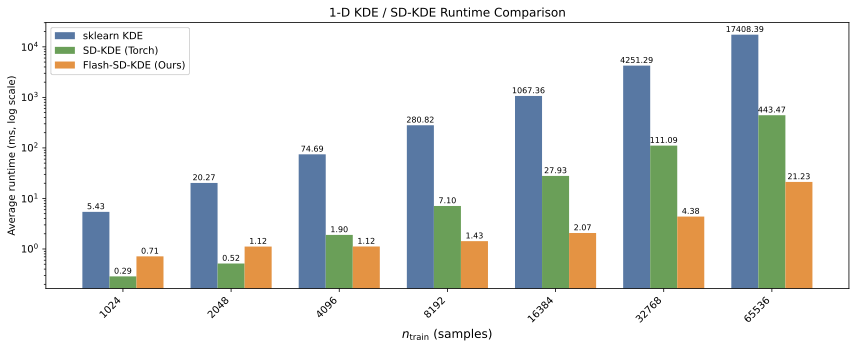
Evidence
The paper reports:
- Large speedups on 16D GPU benchmarks (up to tens of times faster than a Torch baseline).
- End-to-end SD-KDE on million-scale inputs in a few seconds on a single GPU (as stated in the paper).
Limitations and caveats
- The speedups depend on data dimension, batch sizes, and GPU architecture.
- The approach still has quadratic arithmetic cost; it just makes it fast on hardware.
- Accuracy is compared against baselines on synthetic data; broader evaluation is left for future work.
Takeaway
Flash-SD-KDE is a hardware-aware rewrite of SD-KDE that makes a statistically appealing estimator practical at larger scales.