TL;DR
- The manuscript has two parts: a DDPM training derivation and a Bayesian inverse problem case study.
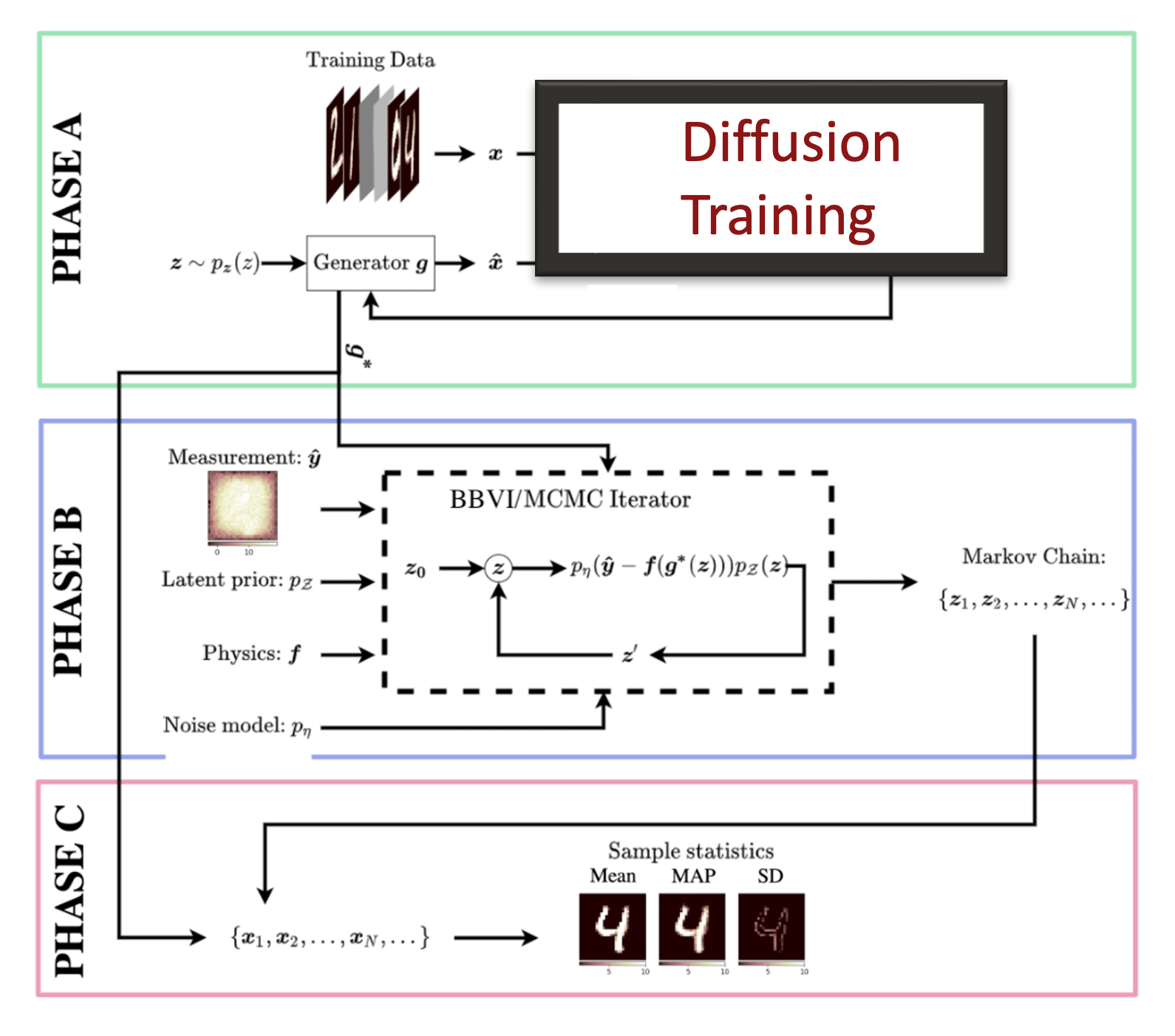
- A latent diffusion model is used as a prior inside Bayesian inversion for an inverse heat conduction task.
- BBVI produces more convincing qualitative results than Metropolis MCMC under the reported setup.
Problem setting
Inverse problems aim to recover unknown inputs to a forward model from observations. The paper focuses on a Bayesian formulation and highlights the challenges of selecting a good prior and sampling in high dimensions.
At a high level, the Bayesian inverse problem can be summarized as:
Key idea
Train a latent diffusion model as a prior, then perform inference in latent space rather than directly in the original parameter space. This makes it possible to leverage a powerful learned prior while keeping inference tractable.
Method (high level)
- Train a latent diffusion model on data.
- Use the learned generator as the prior in a Bayesian inverse problem.
- Compare BBVI and Metropolis MCMC for posterior inference in latent space.

The DDPM training objective used in the derivation can be written as:
Evidence
The paper reports:
- A qualitative inverse heat conduction example where BBVI performs better than the MCMC baseline used.
- A detailed derivation of the DDPM training loss.
Limitations and open points
- Several experimental details are not fully specified (dataset size, exact operator, and full metrics).
- The choice of variational family and MCMC settings is not deeply explored.
Takeaway
The project illustrates how latent diffusion priors can be integrated into Bayesian inversion and suggests that variational methods can be more practical than naive MCMC in this setting.